Sans développer les déterminants, prouvez les identités suivantes. Compléments algébriques et mineurs

Déterminant- ième ordre, correspondant à une matrice carrée d'ordre , s'appelle une somme algébrique membres, composés comme suit : les membres de la somme sont tous les produits possibles éléments de la matrice, pris un dans chaque ligne et dans chaque colonne, et le terme
est pris avec un signe plus si la permutation
contient un nombre pair d'inversions, et avec un signe moins dans le cas contraire. Où inversion Nombres Et s'appelle une situation dans laquelle
, Mais est en réarrangement
Plus tôt que . Pour le déterminant matriciel
nous utiliserons la notation ou
.

Les déterminants du premier, du deuxième et du troisième ordre sont calculés à l'aide de formules qui découlent directement de la définition :

Lors du calcul des déterminants du troisième ordre, il est pratique d'utiliser la « règle des triangles », reflétée dans le schéma suivant :

+ ¾

De la définition du déterminant il résulte que :

Ainsi, le déterminant de la diagonale, haut Et matrices triangulaires inférieureségal au produit des éléments diagonaux.

Propriétés de base des déterminants:

Le déterminant ne change pas lorsqu’il est transposé.

. En réorganisant deux lignes (colonnes), le déterminant change de signe.

. Un déterminant contenant deux lignes (colonnes) égales est égal à zéro.

. Je tombe - les chaînes ( - ème colonne) du déterminant sont présentés comme la somme de deux termes, puis le déterminant entier est présenté comme la somme de deux déterminants, dans laquelle toutes les lignes (colonnes) sauf - ème ( - th), le même que dans le déterminant initial, et - je chaîne ( - la ème colonne) dans le premier déterminant est constitué des premiers termes et dans le second - du second. Par exemple:

. Si tous les éléments d'une certaine ligne (colonne) sont multipliés par un nombre, alors le déterminant sera multiplié par ce nombre. Le facteur commun des éléments d'une ligne (colonne) du déterminant peut être retiré du signe du déterminant. Si tous les éléments du déterminant sont multipliés par le nombre , alors le déterminant sera multiplié par .

. Si l'une des lignes (une des colonnes) du déterminant est constituée de zéros, alors le déterminant est égal à zéro.

. Le déterminant ne change pas si les éléments correspondants de son autre ligne (colonne), multipliés par le même nombre, sont ajoutés aux éléments d'une de ses lignes (colonnes).

Exemple 1. Déterminez le nombre d'inversions dans la permutation 2,3,8,1,4,5,7,6.

Solution. Puisque 2 vient avant 1 dans la permutation, 2 forme une inversion dans la permutation. 3 forme également une inversion, 8 - cinq inversions, car vient avant 1,4,5,7 et 6. En continuant, nous constatons que le nombre total d'inversions dans la permutation

Exemple 2. En utilisant uniquement la définition, calculez le déterminant.

Solution. Selon la définition formelle du déterminant

Écrivons tous les produits non nuls des éléments matriciels et les permutations correspondantes :

Étant donné que

on obtient finalement :

Exemple 3. À l'aide des propriétés, calculez le déterminant
.

Solution. Pour calculer le déterminant, nous utiliserons la méthode de réduction à la forme triangulaire supérieure. La méthode consiste à transformer le déterminant en une forme où tous les éléments situés en dessous de la diagonale principale sont égaux à zéro. Le déterminant résultant est égal au produit des éléments de la diagonale principale.

Réorganisons les première et quatrième lignes du déterminant. Le déterminant va changer de signe :

La première ligne du dernier déterminant multipliée par , ajoutez à sa deuxième ligne ; première ligne multipliée par
, ajouter à la troisième ligne ; première ligne multipliée par
, ajoutez à la quatrième ligne. On a:

Réorganisons les deuxième et troisième lignes du déterminant résultant ; Prenons le facteur commun des éléments de la deuxième rangée au-delà du signe du déterminant. On a:

La deuxième ligne du déterminant multiplié par
, ajouter à la troisième ligne ; deuxième ligne multipliée par
, ajoutez à la quatrième ligne. Nous avons:

Réorganisons les troisième et quatrième lignes. La troisième ligne du déterminant résultant, multipliée par , ajoutez à la quatrième ligne. On arrive au déterminant de la matrice triangulaire supérieure

qui se calcule simplement :

2.2.1 . Sont-ils inclus dans le déterminant ? - ème commande du produit :

2.2.2. Avec quel signe dans le déterminant -la commande comprend les travaux :

2.2.3. Ramasser Et pour que le produit
inclus dans le déterminant - la commande avec un signe plus.

2.2.4. Écrivez (en utilisant la définition) le déterminant du quatrième ordre sous forme développée.

2.2.5. En utilisant uniquement la définition, calculez les déterminants :

2.2.6. Calculez les déterminants :

Où

Où

2.2.7. À l'aide des propriétés, calculez les déterminants :

2.2.8. Sans développer les déterminants, prouvez les identités suivantes :

COMPLÉMENTS ALGÉBRIQUES ET MINEURS

Disons un déterminant du troisième ordre : .

Mineure, correspondant à cet élément un ij le déterminant du troisième ordre est appelé un déterminant du deuxième ordre obtenu à partir d'un déterminant donné en supprimant la ligne et la colonne à l'intersection desquelles se trouve l'élément donné, c'est-à-dire je-ème ligne et jème colonne. Mineurs correspondant à un élément donné un ij nous désignerons M ij.

Par exemple, mineure M12, correspondant à l'élément un 12, il y aura un déterminant , qui est obtenu en supprimant la 1ère ligne et la 2ème colonne de ce déterminant.

Ainsi, la formule définissant le déterminant du troisième ordre montre que ce déterminant est égal à la somme des produits des éléments du 1er rang par leurs mineurs correspondants ; dans ce cas le mineur correspondant à l'élément un 12, est pris avec le signe « – », c'est-à-dire on peut écrire ça

(1)

De même, on peut introduire des définitions des mineurs pour des déterminants de second ordre et d’ordre supérieur.

Introduisons un autre concept.

Complément algébriqueélément un ij le déterminant est appelé son mineur M ij, multiplié par (–1) i+j .

Complément algébrique d'un élément un ij désigné par Un ij.

De la définition on obtient que le lien entre le complément algébrique d'un élément et son mineur s'exprime par l'égalité Un ij= (–1) je+j Mij.

Par exemple,

Exemple. Un déterminant est donné. Trouver Un 13, Un 21, Un 32.

Il est facile de voir qu’en utilisant des additions algébriques d’éléments, la formule (1) peut s’écrire :

De la même manière que cette formule, vous pouvez obtenir le développement du déterminant dans les éléments de n’importe quelle ligne ou colonne.

Par exemple, la décomposition du déterminant en éléments de la 2ème rangée peut être obtenue comme suit. D’après la propriété 2 du déterminant, on a :

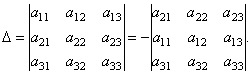
Développons le déterminant résultant dans les éléments de la 1ère ligne.

(2)

D'ici parce que les déterminants du second ordre dans la formule (2) sont des mineurs des éléments un 21, un 22, un 23. Ainsi, c'est-à-dire nous avons obtenu la décomposition du déterminant en éléments de la 2ème rangée.

De même, on peut obtenir le développement du déterminant dans les éléments de la troisième rangée. En utilisant la propriété 1 des déterminants (à propos de la transposition), nous pouvons montrer que des développements similaires sont également valables lors du développement sur des éléments de colonnes.

Le théorème suivant est donc valide.

Théorème (sur le développement d'un déterminant sur une ligne ou une colonne donnée). Le déterminant est égal à la somme des produits des éléments de l'une de ses lignes (ou colonnes) et de leurs compléments algébriques.

Tout ce qui précède est également vrai pour les déterminants de tout ordre supérieur.

Exemples.

MATRICE INVERSE

Le concept de matrice inverse est introduit uniquement pour matrices carrées.

Si UN est une matrice carrée, alors inverse pour cela une matrice est une matrice, notée A-1 et satisfaisant la condition. (Cette définition est introduite par analogie avec la multiplication des nombres)

§ 4. Propriétés des déterminants

Propriété 1. La valeur du déterminant ne changera pas si toutes ses lignes sont remplacées par des colonnes et si chaque ligne est remplacée par une colonne avec le même numéro, c'est-à-dire

=
.

Propriété 2. Réorganiser deux colonnes ou deux lignes d'un déterminant équivaut à le multiplier par - 1. Par exemple,

= -
.

Propriété 3. Si le déterminant a deux colonnes identiques ou deux lignes identiques, alors il est égal à zéro.

Propriété 4. Multiplication de tous les éléments d'une colonne ou d'une ligne d'un déterminant par n'importe quel nombre k équivaut à multiplier le déterminant par ce nombre k. Par exemple,

=k
.

Propriété 5. Si tous les éléments d'une colonne ou d'une ligne sont égaux à zéro, alors le déterminant lui-même est égal à zéro. Cette propriété est un cas particulier de la précédente (pour k = 0).

Propriété 6. Si les éléments correspondants de deux colonnes ou de deux lignes d'un déterminant sont proportionnels, alors le déterminant est égal à zéro.

Propriété 7. Si chaque élément de la nième colonne ou de la nième ligne du déterminant est la somme de deux termes, alors le déterminant peut être représenté comme la somme de deux déterminants, dont l'un est dans la nième colonne, ou, respectivement, dans la nième rangée contient le premier des termes mentionnés, et l'autre contient le second ; les éléments dans les positions restantes sont les mêmes pour les trois déterminants. Par exemple,

=
.+

Propriété 8. Si aux éléments d'une certaine colonne (ou d'une ligne) nous ajoutons les éléments correspondants d'une autre colonne (ou d'une autre ligne), multipliés par un facteur commun, alors la valeur du déterminant ne changera pas. Par exemple,

=
.

D'autres propriétés des déterminants sont liées aux concepts de complément algébrique et de mineur. Le mineur d'un élément est un déterminant obtenu à partir d'un élément donné en barrant la ligne et la colonne à l'intersection desquelles se trouve cet élément.

Le complément algébrique de tout élément du déterminant est égal au mineur de cet élément, pris avec son signe si la somme des nombres de la ligne et de la colonne à l'intersection desquelles se trouve l'élément est un nombre pair, et avec le signe opposé si ce nombre est impair.

On désignera le complément algébrique d'un élément par une lettre majuscule du même nom et du même chiffre que la lettre qui désigne l'élément lui-même.

Propriété 9. Déterminant

 =

est égal à la somme des produits des éléments de n'importe quelle colonne (ou ligne) par leurs compléments algébriques.

En d’autres termes, les égalités suivantes sont vérifiées :

 = a 1 A 1 + a 2 A 2 + a 3 A 3,  = a 1 A 1 + b 1 B 1 + c 1 C 1,

 = b 1 B 1 + b 2 B 2 + b 2 B 2,  = a 2 A 2 + b 2 B 2 + c 2 C 2,

 = c 1 C 1 + c 2 C 2 + c 3 C 3,  = a 3 A 3 + b 2 B 2 + c 3 C 3.

Dans les problèmes 1217-1222, il faut, sans révéler les déterminants, prouver la validité des égalités.

1217.
=
.

Remarque : utilisez la propriété 8.

=
.

Indication : Utiliser la propriété 8.

1219.
=0

Note. Utilisez les propriétés 7, 3, 6.

1220 .
=0

Indication : Utiliser les propriétés 7 et 6.

1221.
=0 1222.
=0

Dans les problèmes 1223-1227, vous devez calculer les déterminants en utilisant une propriété 9.

1223.
. 1224.
.

1225.
. 1226.
.

1227.
.

1228. En utilisant la propriété 8, transformez les déterminants donnés dans les problèmes 1223-1227 de sorte que dans une colonne (ou une ligne) du déterminant, deux éléments deviennent égaux à zéro, puis calculez chacun d'eux en utilisant la propriété 9.

Dans les problèmes 1229-1232, vous devez calculer les déterminants.

1229. . 1230.