Que sont les fonctions zéros ? La réponse est assez simple : il s'agit d'un terme mathématique qui désigne le domaine de définition d'une fonction donnée, dans lequel sa valeur est nulle. Les fonctions zéros sont également appelées. La façon la plus simple d'expliquer ce que sont les fonctions zéros est de donner quelques exemples simples.

Exemples

Considérons l'équation simple y=x+3. Puisque le zéro d'une fonction est la valeur de l'argument auquel y a acquis une valeur nulle, nous substituons 0 sur le côté gauche de l'équation :

Dans ce cas, -3 est le zéro souhaité. Pour une fonction donnée, il n’existe qu’une seule racine de l’équation, mais ce n’est pas toujours le cas.

Regardons un autre exemple :

Remplaçons 0 sur le côté gauche de l'équation, comme dans l'exemple précédent :

Évidemment, dans ce cas il y aura deux zéros de la fonction : x=3 et x=-3. Si l’équation avait un argument du troisième degré, il y aurait trois zéros. Une conclusion simple peut être tirée que le nombre de racines du polynôme correspond au degré maximum de l'argument dans l'équation. Cependant, de nombreuses fonctions, par exemple y = x 3, contredisent à première vue cette affirmation. La logique et le bon sens veulent que cette fonction n'ait qu'un seul zéro - au point x=0. Mais en fait il y a trois racines, elles coïncident toutes. Si vous résolvez l’équation sous une forme complexe, cela devient évident. x=0 dans ce cas, une racine dont la multiplicité est 3. Dans l'exemple précédent, les zéros ne coïncidaient pas, ils avaient donc une multiplicité de 1.

Algorithme de détermination

À partir des exemples présentés, vous pouvez voir comment déterminer les zéros d'une fonction. L'algorithme est toujours le même :

1. Écrivez une fonction.
2. Remplacez y ou f(x)=0.
3. Résolvez l’équation résultante.

La difficulté du dernier point dépend du degré d’argumentation de l’équation. Lors de la résolution d'équations de degrés élevés, il est particulièrement important de se rappeler que le nombre de racines de l'équation est égal au degré maximum de l'argument. Cela est particulièrement vrai pour les équations trigonométriques, où la division des deux côtés par le sinus ou le cosinus entraîne la perte des racines.

Les équations de degré arbitraire sont plus faciles à résoudre en utilisant la méthode de Horner, développée spécifiquement pour trouver les zéros d'un polynôme arbitraire.

La valeur des zéros des fonctions peut être soit négative, soit positive, réelle ou dans le plan complexe, singulière ou multiple. Ou bien il se peut qu’il n’y ait pas de racines à l’équation. Par exemple, la fonction y=8 n’acquerra une valeur nulle pour aucun x, car elle ne dépend pas de cette variable.

L'équation y=x 2 -16 a deux racines, et toutes deux se situent dans le plan complexe : x 1 =4i, x 2 =-4i.

Erreurs courantes

Une erreur courante commise par les écoliers qui n'ont pas encore complètement compris ce que sont les zéros d'une fonction est de remplacer l'argument (x) par zéro, plutôt que par la valeur (y) de la fonction. Ils substituent en toute confiance x=0 dans l’équation et, sur cette base, trouvent y. Mais ce n’est pas la bonne approche.

Une autre erreur, comme déjà mentionné, est la réduction par sinus ou cosinus dans une équation trigonométrique, c'est pourquoi un ou plusieurs zéros de la fonction sont perdus. Cela ne signifie pas que rien ne peut être réduit dans de telles équations, mais dans les calculs ultérieurs, il est nécessaire de prendre en compte ces facteurs « perdus ».

Représentation graphique

Vous pouvez comprendre ce que sont les zéros d'une fonction à l'aide de programmes mathématiques tels que Maple. Vous pouvez y construire un graphique en spécifiant le nombre de points souhaité et l'échelle souhaitée. Les points auxquels le graphique coupe l'axe OX sont les zéros souhaités. C'est l'un des moyens les plus rapides de trouver les racines d'un polynôme, surtout si son ordre est supérieur au tiers. Ainsi, s'il est nécessaire d'effectuer régulièrement des calculs mathématiques, trouver les racines de polynômes de degrés arbitraires, construire des graphiques, Maple ou un programme similaire sera tout simplement indispensable pour effectuer et vérifier les calculs.

Dans lequel il prend la valeur zéro. Par exemple, pour une fonction donnée par la formule

Est nul parce que

.

Les zéros d'une fonction sont aussi appelés racines de la fonction.

La notion de zéros d'une fonction peut être envisagée pour toute fonction dont la plage de valeurs contient zéro ou l'élément zéro de la structure algébrique correspondante.

Pour une fonction d'une variable réelle, les zéros sont les valeurs auxquelles le graphique de la fonction coupe l'axe des x.

Trouver les zéros d'une fonction nécessite souvent l'utilisation de méthodes numériques (par exemple, la méthode de Newton, les méthodes du gradient).

L’un des problèmes mathématiques non résolus consiste à trouver les zéros de la fonction zêta de Riemann.

Racine d'un polynôme

voir également

Littérature

Fondation Wikimédia. 2010.

Voyez ce qu'est « Fonction Zéro » dans d'autres dictionnaires :

Le point où une fonction donnée f(z) disparaît ; ainsi, N.f. f (z) est identique aux racines de l'équation f (z) = 0. Par exemple, les points 0, π, π, 2π, 2π,... sont des zéros de la fonction sinz. Zéros d'une fonction analytique (Voir Analytique... ...

Fonction zéro, fonction zéro... Dictionnaire d'orthographe-ouvrage de référence

Ce terme a d'autres significations, voir Zéro. Il est nécessaire de déplacer le contenu de cet article vers l’article « Fonction Null ». Vous pouvez aider le projet en combinant des articles. S'il est nécessaire de discuter de la faisabilité d'une fusion, remplacez ceci... Wikipédia

Ou chaîne C (du nom du langage C) ou chaîne ASCIZ (du nom de la directive assembleur.asciz), une méthode de représentation de chaînes dans les langages de programmation, dans laquelle, au lieu d'introduire un type de chaîne spécial, un tableau de caractères est utilisé, et à la fin ... ... Wikipedia

Dans la théorie quantique des champs, le nom accepté (jargon) pour la propriété de disparition du facteur de renormalisation de la constante de couplage est où g0 est la constante de couplage nue de l'interaction lagrangienne, physique. constante de couplage déguisée en interaction. Égalité Z... Encyclopédie physique

Mutation nulle n-allèle- Mutation nulle, n. allèle * mutation nulle, n. allèle * mutation nulle ou n. allel ou silencieux a. une mutation conduisant à une perte complète de fonction dans la séquence d'ADN dans laquelle elle s'est produite... La génétique. Dictionnaire encyclopédique

L'énoncé de la théorie des probabilités selon lequel tout événement (appelé événement résiduel), dont l'occurrence est déterminée uniquement par des éléments arbitrairement distants d'une séquence d'événements aléatoires indépendants ou de variables aléatoires, a... ... Encyclopédie mathématique

1) Un nombre qui a la propriété que tout nombre (réel ou complexe) ne change pas lorsqu'on y ajoute. Désigné par le symbole 0. Le produit de n'importe quel nombre par N. est égal à N. : Si le produit de deux nombres est égal à N., alors l'un des facteurs... Encyclopédie mathématique

Fonctions définies par des relations entre variables indépendantes non résolues par rapport à ces dernières ; ces relations sont une des manières de spécifier une fonction. Par exemple, la relation x2 + y2 1 = 0 définit le N.f. ... Grande Encyclopédie Soviétique

Valeurs des arguments z auquel F(z) va à zéro appelé. zéro point, c'est à dire. Si F(un) = 0, alors a - point zéro.

Déf. Point UN appelé commande zéron , Si Le FKP peut être représenté sous la forme F(z) = , où
fonction analytique et
0.

Dans ce cas, dans le développement en série de Taylor de la fonction (43), le premier n les coefficients sont nuls

= =

Etc. Déterminer l'ordre de zéro pour
et (1 –cos z) à z = 0

=
=

zéro 1ère commande

1 – parce que z =
=

zéro 2ème commande

Déf. Point z =
appelé pointer vers l'infini Et zéro les fonctions F(z), Si F(
) = 0. Une telle fonction peut être développée en une série de puissances négatives z : F(z) =
. Si d'abord n les coefficients sont égaux à zéro, alors on arrive à commande zéro n en un point à l'infini : F(z) = z - n
.

Les points singuliers isolés sont divisés en : a) points singuliers amovibles; b) pôles d'ordren; V) points essentiellement singuliers.

Point UN appelé point singulier amovible les fonctions F(z) si à z
un lim F(z) = Avec - numéro final .

Point UN appelé pôle d'ordren (n 1) fonctions F(z), si la fonction inverse
= 1/ F(z) a un ordre nul nà ce point UN. Une telle fonction peut toujours être représentée par F(z) =
, Où
- fonction analytique et
.

Point UN appelé essentiellement un point spécial les fonctions F(z), si à z
un lim F(z) n'existe pas.

Série Laurent

Considérons le cas d'une région de convergence en anneau r < | z 0 – un| < R. centré en un point UN pour la fonction F(z). Présentons deux nouveaux cercles L 1 (r) Et L 2 (R.) près des limites de l'anneau avec une pointe z 0 entre eux. Faisons une coupe de l'anneau, connectons les cercles le long des bords de la coupe, passons à une région simplement connectée et dans

Formule intégrale de Cauchy (39) on obtient deux intégrales sur la variable z

F(z 0) =
+
, (42)

où l’intégration va dans des directions opposées.

Pour l’intégrale sur L 1 condition est remplie | z 0 – un | > | z – un |, et pour l'intégrale sur L 2 condition inverse | z 0 – un | < | z – un |. Par conséquent, le facteur 1/( z – z 0) se développer en série (a) dans l'intégrale sur L 2 et en série (b) dans l'intégrale sur L 1 . On obtient alors le développement F(z) dans la zone de l'anneau dans Série Laurent par des puissances positives et négatives ( z 0 – un)

F(z 0) =
UN n (z 0 -un) n (43)

Où UN n =
=
;UN -n =

Expansion des puissances positives (z 0 - UN) appelé la bonne partie Série Laurent (série Taylor), et l'expansion en puissances négatives est appelée. partie principale Série Laurent.

Si à l'intérieur du cercle L 1 il n’y a pas de points singuliers et la fonction est analytique, alors dans (44) la première intégrale est égale à zéro par le théorème de Cauchy et seule la partie correcte reste dans le développement de la fonction. Les pouvoirs négatifs en expansion (45) n'apparaissent que lorsque l'analyticité est violée à l'intérieur du cercle intérieur et servent à décrire la fonction à proximité de points singuliers isolés.

Construire la série Laurent (45) pour F(z) vous pouvez calculer les coefficients de développement à l'aide d'une formule générale ou utiliser des développements de fonctions élémentaires incluses dans F(z).

Nombre de termes ( n) de la partie principale de la série Laurent dépend du type de point singulier : point singulier amovible (n = 0) ; point essentiellement singulier (n
); pôlen- wow commande(n - numéro définitif).

et pour F(z) = point z = 0 point singulier amovible, parce que il n'y a pas de partie principale. F(z) = (z -
) = 1 -

b) Pour F(z) = point z = 0 - pôle 1er ordre

F(z) = (z -
) = -

c) Pour F(z) = e 1 / z point z = 0 - point essentiellement singulier

F(z) = e 1 / z =

Si F(z) est analytique dans le domaine Dà l'exception de m points singuliers isolés et | z 1 | < |z 2 | < . . . < |z m| , puis lors de l'extension de la fonction en puissances z l'avion entier est divisé en m+ 1 bague | z je | < | z | < | z je+ 1 | et la série Laurent a une apparence différente pour chaque bague. Lors de l'expansion des pouvoirs ( z – z je ) la région de convergence de la série de Laurent est le cercle | z – z je | < r, Où r – distance au point singulier le plus proche.

Etc. Développons la fonction F(z) =dans la série Laurent en pouvoirs z Et ( z - 1).

Solution. Représentons la fonction sous la forme F(z) = - z 2 . Nous utilisons la formule de la somme d'une progression géométrique
. Dans le cercle |z|< 1 ряд сходится и F(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4- . . . , c'est à dire. la décomposition ne contient que correct Partie. Passons à la région extérieure du cercle |z| > 1. Représentons la fonction sous la forme
, où 1/| z| < 1, и получим разложение F(z) = z
=z + 1 +

Parce que , expansion d'une fonction en puissances ( z - 1) on dirait F(z) = (z - 1) -1 + 2 + (z - 1) pour tout le monde
1.

Etc. Développez la fonction dans une série Laurent F(z) =
: a) par degrés z en cercle | z| < 1; b) по степеням z anneau 1< |z| < 3 ; c) по степеням (z – 2).Solution. Décomposons la fonction en fractions simples
= =+=
. Des conditions z =1
UN = -1/2 , z =3
B = ½.

UN) F(z) = ½ [
] = ½ [
-(1/3)
], avec | z|< 1.

b) F(z) = - ½ [
+
] = - (
), à 1< |z| < 3.

Avec) F(z) = ½ [
]= - ½ [
] =

= - ½ = -
, avec |2 - z| < 1

C'est un cercle de rayon 1 centré en z = 2 .

Dans certains cas, les séries entières peuvent être réduites à un ensemble de progressions géométriques, après quoi il est facile de déterminer la région de leur convergence.

Etc. Étudier la convergence de la série

. . . + + + + 1 + () + () 2 + () 3 + . . .

Solution. C'est la somme de deux progressions géométriques avec q 1 = , q 2 = () . Des conditions de leur convergence il résulte < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Fonction est l'un des concepts mathématiques les plus importants. Fonction - dépendance variable àà partir d'une variable X, si chaque valeur X correspond à une seule valeur à. Variable X appelé variable indépendante ou argument. Variable à appelée variable dépendante. Toutes les valeurs de la variable indépendante (variable X) forment le domaine de définition de la fonction. Toutes les valeurs que prend la variable dépendante (variable oui), forment la plage de valeurs de la fonction.

Graphique de fonction appeler l'ensemble de tous les points du plan de coordonnées dont les abscisses sont égales aux valeurs de l'argument et les ordonnées sont égales aux valeurs correspondantes de la fonction, c'est-à-dire les valeurs de la les variables sont portées le long de l'axe des abscisses X, et les valeurs de la variable sont tracées le long de l'axe des ordonnées oui. Pour représenter graphiquement une fonction, vous devez connaître les propriétés de la fonction. Les principales propriétés de la fonction seront discutées ci-dessous !

Pour construire un graphique d'une fonction, nous vous recommandons d'utiliser notre programme - Fonctions graphiques en ligne. Si vous avez des questions en étudiant le contenu de cette page, vous pouvez toujours les poser sur notre forum. Également sur le forum, ils vous aideront à résoudre des problèmes de mathématiques, de chimie, de géométrie, de théorie des probabilités et bien d'autres sujets !

Propriétés de base des fonctions.

1) Domaine fonctionnel et plage de fonctions.

Le domaine d'une fonction est l'ensemble de toutes les valeurs d'arguments valides et valides X(variable X), pour lequel la fonction y = f(x) déterminé.
L'étendue d'une fonction est l'ensemble de toutes les valeurs réelles oui, ce que la fonction accepte.

En mathématiques élémentaires, les fonctions sont étudiées uniquement sur l’ensemble des nombres réels.

2) Zéros de fonction.

La fonction zéro est la valeur de l'argument pour laquelle la valeur de la fonction est égale à zéro.

3) Intervalles de signe constant d'une fonction.

Les intervalles de signe constant d'une fonction sont des ensembles de valeurs d'arguments sur lesquels les valeurs de la fonction sont uniquement positives ou uniquement négatives.

4) Monotonie de la fonction.

Une fonction croissante (dans un certain intervalle) est une fonction dans laquelle une plus grande valeur de l'argument de cet intervalle correspond à une plus grande valeur de la fonction.

Une fonction décroissante (dans un certain intervalle) est une fonction dans laquelle une valeur plus grande de l'argument de cet intervalle correspond à une valeur plus petite de la fonction.

5) Fonction paire (impaire).

Une fonction paire est une fonction dont le domaine de définition est symétrique par rapport à l'origine et pour tout X du domaine de la définition l'égalité f(-x) = f(x). Le graphique d’une fonction paire est symétrique par rapport à l’ordonnée.

Une fonction impaire est une fonction dont le domaine de définition est symétrique par rapport à l'origine et pour tout X du domaine de la définition, l'égalité est vraie f(-x) = - f(x). Le graphique d’une fonction impaire est symétrique par rapport à l’origine.

6) Fonctions limitées et illimitées.

Une fonction est dite bornée s'il existe un nombre positif M tel que |f(x)| ≤ M pour toutes les valeurs de x. Si un tel nombre n’existe pas, alors la fonction est illimitée.

7) Périodicité de la fonction.

Une fonction f(x) est périodique s'il existe un nombre T non nul tel que pour tout x f(x+T) = f(x). Ce plus petit nombre est appelé la période de la fonction. Toutes les fonctions trigonométriques sont périodiques. (Formules trigonométriques).

Après avoir étudié ces propriétés d'une fonction, vous pouvez facilement explorer la fonction et, en utilisant les propriétés de la fonction, vous pouvez créer un graphique de la fonction. Consultez également le matériel sur la table de vérité, la table de multiplication, le tableau périodique, le tableau des dérivées et le tableau des intégrales.

Zéros de fonction

Que sont les fonctions zéros ? Comment déterminer les zéros d'une fonction analytiquement et graphiquement ?

Zéros de fonction- ce sont les valeurs des arguments pour lesquelles la fonction est égale à zéro.

Pour trouver les zéros de la fonction donnée par la formule y=f(x), vous devez résoudre l'équation f(x)=0.

Si l’équation n’a pas de racines, la fonction n’a pas de zéros.

1) Trouvez les zéros de la fonction linéaire y=3x+15.

Pour trouver les zéros de la fonction, résolvez l’équation 3x+15 =0.

Ainsi, le zéro de la fonction est y=3x+15 - x= -5.

2) Trouvez les zéros de la fonction quadratique f(x)=x²-7x+12.

Pour trouver les zéros de la fonction, résolvez l'équation quadratique

Ses racines x1=3 et x2=4 sont des zéros de cette fonction.

3) Trouver les zéros de la fonction

Une fraction a du sens si le dénominateur est différent de zéro. Par conséquent, x²-1≠0, x² ≠ 1, x ≠±1. C'est-à-dire le domaine de définition d'une fonction donnée (DO)

Parmi les racines de l'équation x²+5x+4=0 x1=-1 x2=-4, seul x=-4 est inclus dans le domaine de définition.

Pour trouver les zéros d'une fonction donnée graphiquement, vous devez trouver les points d'intersection du graphe de la fonction avec l'axe des abscisses.

Si le graphique ne coupe pas l’axe Ox, la fonction n’a pas de zéros.

la fonction dont le graphique est représenté sur la figure comporte quatre zéros -

En algèbre, le problème de la recherche des zéros d'une fonction se pose à la fois en tant que tâche indépendante et lors de la résolution d'autres problèmes, par exemple lors de l'étude d'une fonction, de la résolution d'inégalités, etc.

www.algebraclass.ru

Règle des zéros de fonction

Concepts de base et propriétés des fonctions

Règle (droit de) la correspondance. Fonction monotone .

Fonctions limitées et illimitées. Continu et

fonctions discontinues . Fonctions paires et impaires.

Fonction périodique. Période de la fonction.

Zéros de fonction . Asymptote .

Le domaine de définition et la plage de valeurs d'une fonction. En mathématiques élémentaires, les fonctions sont étudiées uniquement sur l'ensemble des nombres réels R. . Cela signifie que l'argument de la fonction ne peut prendre que les valeurs réelles pour lesquelles la fonction est définie, c'est-à-dire il n'accepte également que les valeurs réelles. Un tas de X toutes les valeurs d'argument valides et valides X, pour lequel la fonction oui = F (X) est défini, appelé domaine de la fonction. Un tas de Oui toutes les vraies valeurs oui, que la fonction accepte, est appelé plage de fonctions. Nous pouvons maintenant donner une définition plus précise de la fonction : règle (loi) de correspondance entre ensembles X Et Oui , selon lequel pour chaque élément de l'ensemble X vous pouvez trouver un et un seul élément de l'ensemble Oui, s'appelle une fonction .

De cette définition, il résulte qu'une fonction est considérée comme définie si :

— le domaine de définition de la fonction est spécifié X ;

— la plage de fonctions est spécifiée Oui ;

— la règle (loi) de correspondance est connue, et telle que pour chaque

valeur d’argument, une seule valeur de fonction peut être trouvée.

Cette exigence d'unicité de la fonction est obligatoire.

Fonction monotone. Si pour deux valeurs de l'argument X 1 et X 2 de l'état X 2 > X 1 suit F (X 2) > F (X 1), alors la fonction F (X) est appelé en augmentant; si pour quelque chose X 1 et X 2 de l'état X 2 > X 1 suit F (X 2)

La fonction représentée sur la figure 3 est limitée, mais pas monotone. La fonction de la figure 4 est tout le contraire, monotone, mais illimitée. (Expliquez cela s'il vous plaît !).

Fonctions continues et discontinues. Fonction oui = F (X) est appelé continu à ce point X = un, Si:

1) la fonction est définie lorsque X = un, c'est à dire. F (un) existe ;

2) existe fini limite limite F (X) ;

Si au moins une de ces conditions n’est pas remplie, alors la fonction est appelée explosifà ce point X = un .

Si la fonction est continue pendant tout le monde points de son domaine de définition, alors on l'appelle fonction continue.

Fonctions paires et impaires. Si pour n'importe lequel X du domaine de définition de la fonction, ce qui suit est valable : F (— X) = F (X), alors la fonction est appelée même; si ça arrive : F (— X) = — F (X), alors la fonction est appelée impair. Graphique d'une fonction paire symétrique par rapport à l'axe Y(Fig. 5), un graphique d'une fonction impaire Sim métrique par rapport à l'origine(Fig.6).

Fonction périodique. Fonction F (X) — périodique, si une telle chose existe non nul nombre T pourquoi n'importe lequel X du domaine de définition de la fonction, ce qui suit est valable : F (X + T) = F (X). Ce moins le numéro est appelé période de la fonction. Toutes les fonctions trigonométriques sont périodiques.

Exemple 1. Prouve ce péché X a une période de 2.

Solution : Nous savons que le péché ( x+ 2 n) = péché X, Où n= 0, ± 1, ± 2, …

Par conséquent, l’ajout 2 n pas à l'argument sinus

change sa valeur e. Y a-t-il un autre numéro avec celui-ci

Faisons comme si P.– un tel nombre, c'est-à-dire égalité:

valable pour n'importe quelle valeur X. Mais alors il a

lieu et à X= / 2, c'est-à-dire

péché(/2 + P.) = péché / 2 = 1.

Mais d'après la formule de réduction sin (/ 2 + P.) = cos P.. Alors

des deux dernières égalités il résulte que parce que P.= 1, mais nous

nous savons que cela n'est vrai que lorsque P. = 2 n. Depuis le plus petit

nombre non nul à partir de 2 n est 2, alors ce nombre

et il y a un péché menstruel X. On peut prouver de la même manière que 2

est aussi une période pour parce que X .

Montrer que les fonctions tan X et lit bébé X avoir des règles.

Exemple 2. Quel nombre est la période de la fonction sin 2 X ?

Solution : Considérez le péché 2 X= péché(2 x+ 2 n) = péché [ 2 ( X + n) ] .

On voit qu'ajouter nà l'argumentation X, ne change pas

valeur de la fonction. Le plus petit nombre non nul

depuis n c'est, donc c'est la période sin 2 X .

Fonction zéros. La valeur de l'argument pour laquelle la fonction est égale à 0 est appelée zéro ( racine) fonction. Une fonction peut avoir plusieurs zéros. Par exemple, la fonction oui = X (X + 1) (X- 3) a trois zéros : X = 0, X = — 1, X= 3. Géométriquement fonction nulle – c'est l'abscisse du point d'intersection du graphe de fonction avec l'axe X .

La figure 7 montre un graphique d'une fonction avec des zéros : X = un , X = b Et X = c .

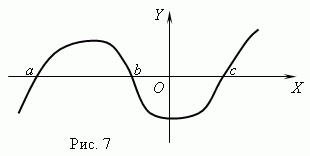
Asymptote. Si le graphique d'une fonction s'approche indéfiniment d'une certaine ligne à mesure qu'elle s'éloigne de l'origine, alors cette ligne est appelée asymptote.

Sujet 6. «Méthode d'intervalle».

Si f (x) f (x 0) pour x x 0, alors la fonction f (x) est appelée continu au point x 0.

Si une fonction est continue en tout point d’un intervalle I, alors elle est appelée continu sur l'intervalle I (l'intervalle I s'appelle intervalle de continuité de la fonction). Le graphique d’une fonction sur cet intervalle est une ligne continue, qui, dit-on, peut être « tracée sans retirer le crayon du papier ».

Propriété des fonctions continues.

Si sur l'intervalle (a ; b) la fonction f est continue et ne s'annule pas, alors elle conserve un signe constant sur cet intervalle.

Une méthode de résolution des inégalités à une variable, la méthode des intervalles, est basée sur cette propriété. Soit la fonction f(x) être continue sur l'intervalle I et disparaître en un nombre fini de points dans cet intervalle. Par la propriété des fonctions continues, ces points divisent I en intervalles, dans chacun desquels la fonction continue f(x) c maintient un signe constant. Pour déterminer ce signe, il suffit de calculer la valeur de la fonction f(x) en un point quelconque de chacun de ces intervalles. Sur cette base, nous obtenons l'algorithme suivant pour résoudre les inégalités à l'aide de la méthode des intervalles.

Méthode d'intervalle pour les inégalités de la forme

Trouver le domaine de définition de la fonction f(x) ;

Trouver les zéros de la fonction f(x) ;

Tracez le domaine de définition et les zéros de la fonction sur la droite numérique. Les zéros d'une fonction divisent son domaine de définition en intervalles dans chacun desquels la fonction conserve un signe constant ;

Trouvez les signes de la fonction dans les intervalles résultants en calculant la valeur de la fonction en un point quelconque de chaque intervalle ;

Écrivez la réponse.

Méthode d'intervalle. Niveau moyen.

Voulez-vous tester votre force et connaître le résultat de votre préparation à l'examen d'État unifié ou à l'examen d'État unifié ?

Fonction linéaire

Une fonction de la forme est dite linéaire. Prenons une fonction comme exemple. Il est positif à 3″> et négatif à. Le point est le zéro de la fonction (). Montrons les signes de cette fonction sur l'axe des nombres :

On dit que « la fonction change de signe en passant par le point ».

On voit que les signes de la fonction correspondent à la position du graphe de la fonction : si le graphe est au dessus de l'axe, le signe est « », si en dessous il est « ».

Si l'on généralise la règle résultante à une fonction linéaire arbitraire, on obtient l'algorithme suivant :

Trouver le zéro de la fonction ;

Nous le marquons sur l'axe des nombres ;

Nous déterminons le signe de la fonction sur les côtés opposés de zéro.

Fonction quadratique

J'espère que vous vous souvenez comment résoudre les inégalités quadratiques ? Sinon, lisez le sujet « Inégalités quadratiques ». Je vous rappelle la forme générale d'une fonction quadratique : .

Rappelons maintenant quels signes prend la fonction quadratique. Son graphique est une parabole, et la fonction prend le signe " " pour ceux dans lesquels la parabole est au dessus de l'axe, et " " - si la parabole est en dessous de l'axe :

Si une fonction a des zéros (valeurs auxquelles), la parabole coupe l'axe en deux points - les racines de l'équation quadratique correspondante. Ainsi, l'axe est divisé en trois intervalles, et les signes de la fonction changent alternativement en passant par chaque racine.

Est-il possible de déterminer les signes d'une manière ou d'une autre sans dessiner une parabole à chaque fois ?

Rappelons qu'un trinôme carré peut être factorisé :

Marquons les racines sur l'axe :

On rappelle que le signe d'une fonction ne peut changer qu'en passant par la racine. Utilisons ce fait : pour chacun des trois intervalles dans lesquels l'axe est divisé par des racines, il suffit de déterminer le signe de la fonction en un seul point arbitrairement choisi : aux points restants de l'intervalle le signe sera le même .

Dans notre exemple : à 3″> les deux expressions entre parenthèses sont positives (remplacez, par exemple : 0″>). On met un signe « » sur l'axe :

Eh bien, lorsque (substitut, par exemple), les deux parenthèses sont négatives, ce qui signifie que le produit est positif :

C'est ce que c'est méthode d'intervalle: connaissant les signes des facteurs sur chaque intervalle, on détermine le signe du produit entier.

Considérons également les cas où la fonction n'a pas de zéros, ou un seul.

S’ils ne sont pas là, alors il n’y a pas de racines. Cela signifie qu’il n’y aura pas de « passage par la racine ». Cela signifie que la fonction ne prend qu'un seul signe sur toute la droite numérique. Il peut être facilement déterminé en le substituant à une fonction.

S'il n'y a qu'une seule racine, la parabole touche l'axe, donc le signe de la fonction ne change pas en passant par la racine. Quelle règle pouvons-nous proposer pour de telles situations ?

Si vous factorisez une telle fonction, vous obtenez deux facteurs identiques :

Et toute expression au carré est non négative ! Le signe de la fonction ne change donc pas. Dans de tels cas, nous soulignerons la racine, au passage par laquelle le signe ne change pas, en l'entourant d'un carré :

Nous appellerons une telle racine multiples.

Méthode d'intervalle dans les inégalités

Désormais, toute inégalité quadratique peut être résolue sans dessiner de parabole. Il suffit de placer les signes de la fonction quadratique sur l'axe et de sélectionner des intervalles en fonction du signe de l'inégalité. Par exemple:

Mesurons les racines sur l'axe et plaçons les signes :

Nous avons besoin de la partie de l'axe avec le signe " " ; puisque l'inégalité n'est pas stricte, les racines elles-mêmes sont également incluses dans la solution :

Considérons maintenant une inégalité rationnelle – une inégalité dont les deux côtés sont des expressions rationnelles (voir « Équations rationnelles »).

Exemple:

Tous les facteurs sauf un sont ici « linéaires », c’est-à-dire qu’ils contiennent une variable uniquement à la puissance première. Nous avons besoin de tels facteurs linéaires pour appliquer la méthode des intervalles - le signe change en passant par leurs racines. Mais le multiplicateur n’a aucune racine. Cela signifie qu'il est toujours positif (vérifiez cela par vous-même) et n'affecte donc pas le signe de l'ensemble de l'inégalité. Cela signifie que nous pouvons diviser les côtés gauche et droit de l'inégalité par celle-ci, et ainsi nous en débarrasser :

Maintenant, tout est comme avec les inégalités quadratiques : nous déterminons à quels points chacun des facteurs devient nul, marquons ces points sur l'axe et disposons les signes. Je voudrais attirer votre attention sur un fait très important :

Dans le cas d'un nombre pair, on fait la même chose que précédemment : on entoure le point d'un carré et on ne change pas de signe en passant par la racine. Mais dans le cas d'un nombre impair, cette règle ne s'applique pas : le signe changera quand même en passant par la racine. Par conséquent, nous ne faisons rien de plus avec une telle racine, comme s'il ne s'agissait pas d'un multiple. Les règles ci-dessus s'appliquent à toutes les puissances paires et impaires.

Que devons-nous écrire dans la réponse ?

Si l'alternance des signes est violée, il faut être très prudent, car si l'inégalité n'est pas stricte, la réponse doit inclure tous les points ombrés. Mais certains d’entre eux se démarquent souvent, c’est-à-dire qu’ils ne sont pas inclus dans la zone ombrée. Dans ce cas, nous les ajoutons à la réponse sous forme de points isolés (entre accolades) :

Exemples (décidez vous-même) :

Réponses:

1. Si parmi les facteurs c'est simple, c'est une racine, car on peut la représenter comme.
   .

2. Trouvons les zéros de la fonction.

f(x) à x .

Répondre f(x) à x .

2) x2 >-4x-5 ;

x2 +4x +5>0 ;

Soit f(x)=x 2 +4x +5 puis Trouvons tel x pour lequel f(x)>0,

D=-4 Pas de zéros.

4. Systèmes d'inégalités. Inégalités et systèmes d'inégalités à deux variables

1) L'ensemble des solutions à un système d'inégalités est l'intersection des ensembles de solutions aux inégalités qui le composent.

2) L'ensemble des solutions à l'inégalité f(x;y)>0 peut être représenté graphiquement sur le plan de coordonnées. Typiquement, la droite définie par l'équation f(x;y) = 0 divise le plan en 2 parties, dont l'une est la solution de l'inégalité. Pour déterminer quelle partie, vous devez substituer les coordonnées d'un point arbitraire M(x0;y0) qui ne se trouve pas sur la ligne f(x;y)=0 dans l'inégalité. Si f(x0;y0) > 0, alors la solution de l'inégalité est la partie du plan contenant le point M0. si f(x0;y0)<0, то другая часть плоскости.

3) L'ensemble des solutions à un système d'inégalités est l'intersection des ensembles de solutions aux inégalités qui le composent. Soit par exemple un système d'inégalités :

.

Pour la première inégalité, l'ensemble des solutions est un cercle de rayon 2 et centré à l'origine, et pour la seconde, c'est un demi-plan situé au dessus de la droite 2x+3y=0. L'ensemble des solutions de ce système est l'intersection de ces ensembles, c'est-à-dire demi-cercle.

4) Exemple. Résoudre le système d'inégalités :

La solution de la 1ère inégalité est l'ensemble, la 2ème est l'ensemble (2;7) et la troisième est l'ensemble.

L'intersection de ces ensembles est l'intervalle (2;3], qui est l'ensemble des solutions du système d'inégalités.

5. Résoudre des inégalités rationnelles à l'aide de la méthode des intervalles

La méthode des intervalles est basée sur la propriété suivante du binôme (x-a) : le point x = α divise l'axe des nombres en deux parties - à droite du point α le binôme (x-α)>0, et à la à gauche du point α (x-α)<0.

Supposons qu'il soit nécessaire de résoudre l'inégalité (x-α 1)(x-α 2)...(x-α n)>0, où α 1, α 2 ...α n-1, α n sont fixes nombres parmi lesquels il n'y a pas d'égaux, et tels que α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 en utilisant la méthode des intervalles, procédez comme suit : les nombres α 1, α 2 ...α n-1, α n sont portés sur l'axe numérique ; dans l'intervalle à droite du plus grand d'entre eux, c'est-à-dire nombres α n, mettez un signe plus, dans l'intervalle qui le suit de droite à gauche mettez un signe moins, puis un signe plus, puis un signe moins, etc. Alors l'ensemble de toutes les solutions de l'inégalité (x-α 1)(x-α 2)...(x-α n)>0 sera l'union de tous les intervalles dans lesquels le signe plus est placé, et l'ensemble de solutions à l'inégalité (x-α 1 )(x-α 2)...(x‑α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».

1) Résoudre des inégalités rationnelles (c'est-à-dire des inégalités de la forme P(x) Q(x) où sont des polynômes) est basé sur la propriété suivante d'une fonction continue : si une fonction continue disparaît aux points x1 et x2 (x1 ; x2) et n'a pas d'autres racines entre ces points, alors dans le intervalles (x1; x2) la fonction conserve son signe.

Par conséquent, pour trouver les intervalles de signe constant de la fonction y=f(x) sur la droite numérique, marquez tous les points auxquels la fonction f(x) disparaît ou subit une discontinuité. Ces points divisent la droite numérique en plusieurs intervalles, à l'intérieur de chacun desquels la fonction f(x) est continue et ne disparaît pas, c'est-à-dire enregistre le signe. Pour déterminer ce signe, il suffit de trouver le signe de la fonction en tout point de l'intervalle considéré de la droite numérique.

2) Déterminer les intervalles de signe constant d'une fonction rationnelle, c'est-à-dire Pour résoudre une inégalité rationnelle, on marque sur la droite numérique les racines du numérateur et les racines du dénominateur, qui sont aussi les racines et les points de rupture de la fonction rationnelle.

Résoudre les inégalités à l'aide de la méthode des intervalles

3. < 20.

Solution. La plage des valeurs acceptables est déterminée par le système d'inégalités :

Pour la fonction f(x) = – 20. Trouver f(x) :

d'où x = 29 et x = 13.

f(30) = – 20 = 0,3 > 0,

f(5) = – 1 – 20 = – 10< 0.

Répondre: . Méthodes de base pour résoudre des équations rationnelles. 1) Le plus simple : résolu par les simplifications habituelles - réduction à un dénominateur commun, réduction de termes similaires, etc. Les équations quadratiques ax2 + bx + c = 0 sont résolues par...

X change sur l'intervalle (0,1], et diminue sur l'intervalle)